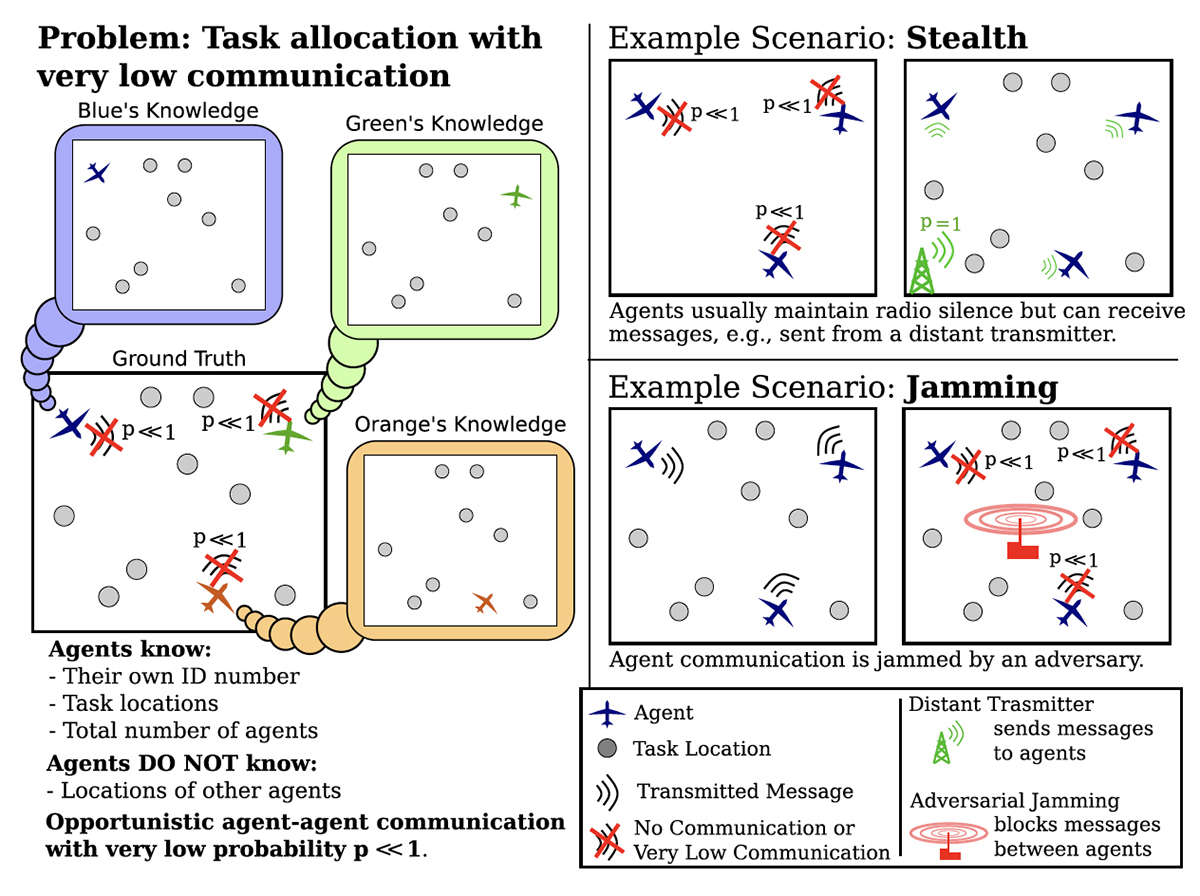
News Story
Nonlinear control design for a school of robotic fish

A school of robotic fish serves as a testbed for formation control experiments at the University of Maryland’s Neutral Buoyancy Research Facility. (Fig. 1 from the paper)
A new paper from the Collective Dynamics and Control Laboratory (CDCL) presents a nonlinear control design for the stabilization of parallel and circular motion in a model school of robotic fish. Planar Formation Control of a School of Robotic Fish was written by alumnus Paul Ghanem (MSSE 2019), Aerospace Engineering Postdoctoral Researcher Artur Wolek, and Professor Derek Paley (AE/ISR), the director of the Maryland Robotics Center.
Collective behavior of mobile agents has received significant interest recently in fields such as biology, physics, computer science, and control engineering. Research in this area is allowing scientists to better understand swarming behavior in nature and benefits control engineers in numerous applications by mimicking nature’s behavior in engineered mobile systems such as unmanned ground, air, and underwater vehicles.
CDCL recently investigated the design, sensing, and control of a single fish-inspired robot driven by an internal rotor. In this new paper, the group presents control laws that stabilize planar formations of a school of robotic fish. Challenges in underwater sensing and communication, especially for small, low-power robotic fish, motivate the use of consensus control to achieve collective motions by communicating only with nearby agents.
Closed-loop swimming dynamics of the fish robots are represented by the canonical Chaplygin sleigh—a nonholonomic mechanical system driven by an internal rotor. The fish robots exchange relative state information according to a connected, undirected communication graph and form a system of coupled, nonlinear, second-order oscillators. Prior work on collective motion of constant-speed, self-propelled particles serves as the foundation of the approach. However, unlike the self-propelled particle, the fish robots follow limit-cycle dynamics to sustain periodic flapping for forward motion with a varying speed. Parallel and circular motions are achieved in an average sense. The proposed control laws do not include feedback linearization of the agents’ dynamics.
The control design approach extends prior work on collective motion of self-propelled particles to a school of robotic fish with Chaplygin sleigh dynamics. The feedback control laws rely only on relative-state measurements between agents that interact according to a connected, undirected, communication graph, and do not include feedback linearization of the agents’ dynamics.
Published April 29, 2020